
Informatique industrielle : Les automates.
Jacques Weber Souhil Megherbi
Table des matières

Informatique industrielle : Les automates.

Jacques Weber Souhil Megherbi
Table des matières
1 Où trouve-t-on des automates ?
1.1 Les organes de commande *
1.1.1 Un digicode *
1.1.2 Un monte-charge *
1.1.3 Récapitulons *
1.2 La gestion des ressources *
1.3 La conception des circuits numériques *
2 Etat et transitions, conditions et actions
2.1 L’état : la mémoire du système *
2.2 Les transitions : l’évolution du système *
2.3 Les conditions : les événements du monde extérieur *
2.4 Où l’on retrouve le monte-charge *
2.5 Les actions : la sortie vers le monde extérieur *
2.6 Quelques règles de grammaire *
3.1 Etats et variables *
3.2 Transitions et fonctions *
4.1 Horloge, registre d’état et transitions *
4.1.1 Le registre d’état *
4.1.2 Le rôle de l’horloge *
4.1.3 Les diagrammes de transitions (retour) *
4.1.4 Une approche algorithmique : VHDL *
4.2 Des choix d’architecture décisifs *
4.2.1 Calculs des sorties : machines de Mealy et de Moore *
4.2.2 Codage des états *
4.2.3 Synchronisations des entrées et des sorties *
Informatique industrielle : Les automates.
Cette partie du cours d’informatique industrielle joue un rôle charnière ; nous allons y découvrir des objets abstraits : les automates. Parfois appelés, suivant les origines de l’auteur du texte qui les décrit automates finis (les théoriciens de l’automatique et des réseaux), machines à nombre fini d’états (les concepteurs de circuits numériques), séquenceurs (les concepteurs d’unités centrales d’ordinateurs et certains automaticiens) ces objets peuvent être réalisés par du matériel, des circuits, ou du logiciel, des programmes, ou par un savant mélange des deux ingrédients précédents.
Cette ubiquité (matériel et logiciel) conduit actuellement à développer des outils communs de conception, qui décrivent de façon homogène des applications qui seront ensuite réalisées soit par du logiciel, si la vitesse des processeurs le permet, soit par des circuits spécialisés si la vitesse de traitement demandée dépasse les capacités des processeurs. Autre domaine d’application non négligeable : il faut bien, dans tous les cas, réaliser matériellement les processeurs eux-mêmes !
La réponse est simple : partout. La commande d’un ascenseur ou d’un feu tricolore à un carrefour routier est un automate, un digicode est un automate, le bus PCI de vos PC est dirigé par des automates, TCP que vous utilisez sans le savoir ou en le sachant, quand vous surfez sur internet, est un automate, UNIX est un ensemble d’automates etc.
On peut utiliser un automate dans toutes les applications où la gestion d’un processus, l’utilisation d’une ressource, un traitement sur de données peuvent être décrits par une chronologie qui fait intervenir un nombre fini d’opérations distinctes conditionnées par des entrées extérieures.
Prenons quelques exemples.
Comme premiers exemples nous prendrons deux applications très simples (ou simplifiées, comme on voudra), bien connue de tous : un digicode tel qu’on en voit aux portes d’entrées des immeubles et une commande de monte-charge, pour ne pas parler d’ascenseur par modestie.
Un digicode est constitué d’un clavier à 16 touches qui constitue l’organe d’entrée d’un automate dont l’unique sortie commande l’ouverture d’une porte. Nous nous restreindrons à un digicode rudimentaire dans lequel le code secret est fixé une fois pour toutes, sans modification possible.
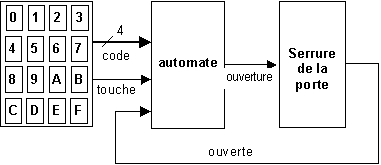
Imaginons, par exemple, que l’ouverture de la porte soit obtenue en fournissant le code C94 (comme cachan + département). Evidemment l’automate doit être informé du fait que l’utilisateur a ouvert la porte, c’est le rôle du signal " ouverte ". Le travail de l’automate peut être résumé par le diagramme suivant :
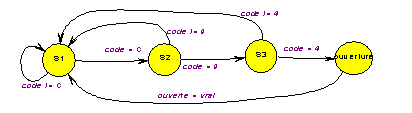
Du moins en première approximation ; il est clair que l’automate doit avoir un moyen de séparer les frappes sur les différentes touches, il doit donc attendre entre deux touches que l’utilisateur relâche le clavier :
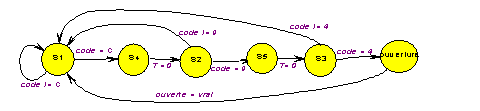
en admettant que l’absence de frappe d’une touche provoque T = 0.
Deuxième exemple d’introduction : la commande d’un monte-charge rudimentaire.
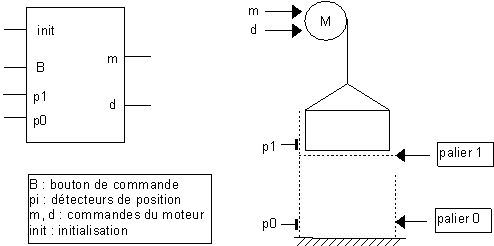
Le moteur est commandé par deux signaux m et d pour montée et descente. La commande élabore ces commandes à partir de ses entrées B, p1, p0 et init suivant le cahier des charges suivant :
Le fonctionnement de l’automate peut être décrit par le diagramme :
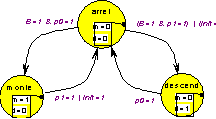
On notera que le cahier des charges a dû être précisé lors de l’élaboration du diagramme : l’entrée init n’inverse pas brutalement la commande du moteur, elle force un passage à l’arrêt.
Ces exemples illustrent quelques concepts de base :
Les dessins que nous avons utilisés pour illustrer nos exemples s’appellent diagrammes de transitions (state transition diagrams, STD). Très utilisés, on les rencontre sous de nombreuses variantes assez similaires. Les automaticiens de langue française utilisent beaucoup une représentation voisine, connue sous le nom de GRAFCET (graphe de commande étape transition).
Il existe de nombreux outils de conception assistée par ordinateur qui emploient ces diagrammes, recherchez Statecad sur Internet pour en être convaincu, ces outils comportent généralement une traduction automatique des diagrammes en langage C, VHDL, Verilog ou autre.
Deux remarques :
Une autre application classique des automates est d’aider à la gestion d’une ressource, c’est à dire à surveiller le bon usage d’un élément qui ne peut pas être utilisé n’importe comment. Les exemples abondent dans le domaine informatique : accès à un réseau, à un périphérique partagé comme une imprimante, ou contrôle d’une zone mémoire organisée en file (fifo, pour first in first out) ou tampon.
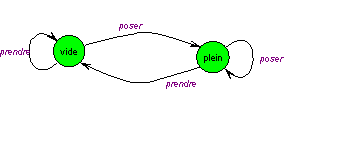
Prenons à titre d’illustration ce dernier exemple. Une mémoire FIFO est une zone mémoire de taille généralement fixe destinée à assurer la synchronisation des échanges de données entre une source (le producteur) et un destinataire (le consommateur) dont les vitesses de transfert ne sont pas égales à chaque instant. Le rôle de l’automate est justement d’assurer une vitesse moyenne de transfert égale de chaque côté :
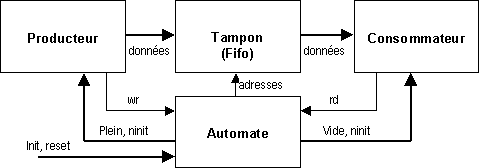
En simplifiant notablement, on peut résumer le fonctionnement comme suit :
Le rôle de l’automate n’est pas ici de commander une application au sens propre du terme, mais de faciliter l’utilisation d’une ressource.
Un exemple de diagramme de transitions réalisant un automate simplifié pourrait être :
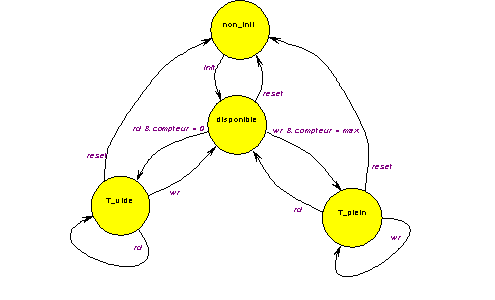
Dans ce type de problème l’usage d’un automate, qui pourrait être ici purement logiciel, peut sembler plus lourde qu’une gestion directe du tampon. Cela serait vrai si le producteur et le consommateur appartenaient au même programme séquentiel. Cette situation n’est évidemment jamais le cas, producteur et consommateur sont deux programmes indépendants, voire deux machines indépendantes. L’utilisation d’un automate facilite alors la gestion du parallélisme (fonctionnement indépendant de chacune des parties), c’est pour répondre à ce type de difficulté qu’ils ont été inventés.
Pour ceux qui souhaiteraient un exemple du même ordre mais non informatique, la situation ressemble à la gestion des barrières d’accès à un parking : il faut éviter de mettre plus de voitures que le parking n’en contient (le parking vide ne pose guère de problème).
Dernier domaine évoqué dans cette introduction : la conception des circuits numériques eux-mêmes.
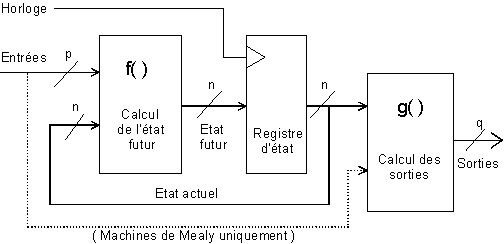
Le schéma bloc qui précède donne la structure générale de pratiquement n’importe quelle fonction logique séquentielle synchrone. Il suffit de dire que le registre d’état, une assemblée de bascules D, passe d’un état à un autre à chaque front du signal d’horloge, en fonction des entrées extérieures. Nous n’avons là rien d’autre que la matérialisation d’un automate dont les transitions sont conditionnées par l’horloge. Mais n’anticipons pas.
Les diagrammes de transitions constituent un langage ; bien que graphique, ce langage doit être dépourvu de toute ambiguïté, il doit donc respecter une grammaire. Ce langage graphique est utile à la compréhension si on en possède bien la signification. Grammaire et sens sont l’objet des quelques précisions qui suivent.
L’état d’un automate constitue la mémoire du système, il contient le résultat des événements précédents et de leur chronologie ; pour reprendre l’exemple du digicode, chaque état (sauf le premier) contient le fait que l’utilisateur a jusqu’ici appuyé sur les bonnes touches, dans le bon ordre. De façon générale, l’intérêt de l’approche " automate " est que l’on mémorise de façon explicite l’historique des entrées d’un système, la longueur des séquences mémorisées apparaît directement sur le diagramme de transitions.
Les différentes valeurs possibles de l’état du système sont matérialisées par une variable discrète : un nombre entier ou un type énuméré. Peu importe pour l’instant le détail du codage, l’essentiel est que toutes les valeurs possibles de l’état soient distinctes, cela exclut notamment l’emploi d’un nombre flottant pour représenter l’état de l’automate.
Le passage d’un état à un autre est une transition. Une transition matérialise une relation entre l’état actuel, l’état futur et une condition. On peut formellement résumer ceci par une équation de récurrence, en notant Etat(t) la valeur de l’état actuel, celle qui précède une transition, et Etat(t + 1) la valeur de l’état futur, celle qui suit une transition :
Etat(t + 1) = fonction(Etat(t), conditions(t))
Bien qu’un peu vague, l’introduction du temps sous forme d’une variable symbolique ‘t’ illustre le lien entre l’évolution du système et les transitions. Il est essentiel de noter qu’une transition peut s’effectuer si, simultanément :
Les conditions dépendent du monde extérieur, elles sont liées aux entrées que surveille l’automate.
Il est clair que si n’importe quelle entrée peut provoquer une transition n’importe quand, on se heurte à une difficulté non négligeable qui est que la variable " t " précédente, qui symbolise le temps, n’a pas d’unité de mesure fixe. Pire, si plusieurs entrées pilotent le système, on peut assister à des évolutions radicalement différentes pour des écarts de chronologies minimes entre deux suites d’événements extérieurs. Une façon simple de contrôler (pas de supprimer) cette difficulté est d’introduire un cadencement régulier : on impose à l’automate de ne pouvoir changer d’état qu’à des instants prédéterminés par une horloge extérieure. On définit ainsi un automate synchrone.
Les signaux en provenance du monde extérieur n’ont pas toujours le bon goût d’être cohérents entre eux, ils proviennent généralement de sources indépendantes qui ne sont pas coordonnées, qui peuvent même être contradictoires ; le but de l’automate est justement de lever les ambiguïtés, d’imposer une coordination.
Pour illustrer ce qui précède, modifions un peu notre exemple du monte-charge pour le rapprocher d’une commande d’ascenseur : l’automate qui pilote les moteurs reçoit deux ordres en provenance de l’extérieur, " haut " et " bas ", qui indiquent respectivement qu’il y a un appel en provenance d’un étage supérieur à celui où est la cabine, ou un appel en provenance d’un étage inférieur. Quand la cabine atteint le niveau appelant, ces deux entrées reviennent à 0.
Le diagramme de transitions associé pourrait être :
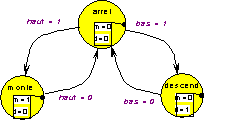
Ce diagramme est faux : quand l’ascenseur est arrêté on ne sait pas ce qu’il doit faire si les deux conditions " haut " et " bas " deviennent vraies simultanément. La situation est certes rare dans le cas d’un ascenseur, mais il faut lever le doute, en imposant, par exemple, une priorité : on privilégie la descente.
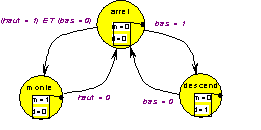
Il reste qu’entre celui qui veut monter et celui qui veut descendre le plus rapide gagne, la première demande est servie. Si pour le départ cela n’est guère injuste, à l’arrivée l’absence de cadencement peut poser quelque problème, à peine arrivée au palier du premier appel, la cabine risque de repartir pour servir le second. Une solution est évidemment d’introduire une temporisation dans l’état d’arrêt :
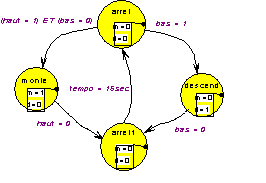
Comme quoi un simple diagramme de transitions a pour le moins le mérite de permettre la discussion de tous les cas de figure.
Sa traduction en un programme en C est quasi immédiate (cible coldfire, entrées sorties sur un port parallèle) :
typedef enum {arret, descend, Init, monte} Sreg0_type ;
typedef volatile unsigned char VU8;
#define HAUT 2
#define BAS 1
void main(void)
{
Sreg0_type Sreg0 = Init ;
int p0, p1, appel ;
unsigned char entree ;
VU8 * ppddr_ptr = (VU8*)0x100001C5;
VU8* ppdat_ptr = (VU8*)0x100001C9;
*ppddr_ptr = 0x03;
/* port parallèle : x-x-x-appel-p1-p0-haut-bas */
while(1)
{
entree = *ppdat_ptr;
p0 = (entree >> 2) && 1 ;
p1 = (entree >> 3) && 1 ;
appel = (entree >> 4) && 1 ;
switch (Sreg0 )
{
case arret :
*ppdat_ptr = 0 ;
if(appel && !p1) Sreg0 = monte;
else if(appel && !p0 ) Sreg0 = descend;
break;
case descend :
*ppdat_ptr = BAS ;
if( p0 ) Sreg0 <= arret;
break ;
case Init :
*ppdat_ptr = 0 ;
if (!p0) Sreg0 <= descend;
else if( p0 ) Sreg0 <= arret;
break;
case monte :
*ppdat_ptr = HAUT ;
if( p1 ) Sreg0 <= arret;
break;
}
}
}
Nous laisserons en l’état notre ascenseur, de nombreux détails restent à régler : mémorise-t-on les appels, surveille-t-on les portes, … ?
Un automate est un organe de commande, il fournit au processus commandé des ordres : ouvrir une porte (digicode), mettre en marche un moteur (ascenseur), incrémenter un pointeur (FIFO). La méthode la plus directe est d’attacher à chaque état les actions qui lui correspondent, de façon systématique, on obtient une machine de MOORE. Dans les exemples précédents les valeurs des sorties étaient systématiquement notées dans les symboles des états, c’est une méthode qui a l’avantage d’être simple et claire, mais qui peut devenir lourde. Dans un automate câblé (circuits logiques) cette approche consiste à créer une fonction combinatoire de calcul des sorties en fonction de l’état de l’automate. Dans un automate programmé elle consiste à recalculer systématiquement toutes les sorties après chaque transition.
Une autre approche consiste à mémoriser les sorties : les actions de l’automate consitent alors à préciser uniquement les modifications des sorties quand c’est nécessaire. Cette solution est intéressante pour des sorties qui conservent la même valeur pour plusieurs états de l’automate (revoir le digicode ou les deux états d’arrêt de la dernière version de l’ascenseur).
Rien n’interdit non plus de calculer les sorties en fonction de l’état de l’automate et des entrées, cela reviendrait, dans l’exemple de l’ascenseur, à mettre en marche le moteur dès que le bouton d’appel est enfoncé, sans attendre que l’automate ait changé d’état. Les sorties sont alors calculées de la même façon que les transitions : c’est une machine de MEALY.
Résumons les questions à se poser pour le calcul des sorties :
Les principales règles d’écriture d’un diagramme de transitions peuvent se résumer par deux remarques de bon sens :
Traduites sur les diagrammes de transition :
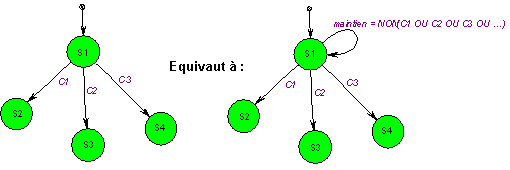
La condition de maintien dans un état est le complément de la réunion de toutes les conditions de sortie (règle 1). Cette condition de maintien étant connue dès que les transitions le sont, elle n’est généralement pas écrite, il y a mémorisation implicite de l’état.
Les conditions de sortie d’un état doivent être mutuellement exclusives :

Attention, les outils automatiques de traitement des diagrammes de transitions ne contrôlent pas toujours que cette dernière condition est vérifiée, dans ce cas ils génèrent une priorité implicite qui dépend de l’ordre dans lequel on a créé le diagramme, ce qui est particulièrement pervers.
Si une transition n’est assortie d’aucune condition, elle est effectuée dès que l’état de départ est " achevé ". Dans un automate logiciel cela veut dire dès que les appels aux fonctions correspondant à l’état considéré sont terminés, dans un automate câblé synchrone au front d’horloge suivant, dans un automate câblé asynchrone c’est une situation absurde.
Dans une première approche nous nous limiterons à des programmes séquentiels simples qui réalisent des automates par un algorithme de boucle sans fin ou par une fonction appelée par un programme principal. Pour les " gourous " cela veut dire que nous ne parlerons pas, dans cette partie, de ce que l’on appelle en informatique les interruptions : événements extérieurs capables de déclencher l’exécution d’une fonction qui n’est " appelée " par aucun programme.
Un automate sera donc constitué d’un moteur (la boucle sans fin, par exemple) qui est chargée de matérialiser le parcours du diagramme de transitions. Ce moteur suit un algorithme immuable qui peut être résumé par quelque chose du genre (dans le cas d’une boucle) :
Initialiser l’automate
Pour toujours
Lire les entrées
Calculer l’état futur
Mettre à jour l’état
Calculer les sorties en fonction de l’état
Si temporisation attendre fin de tempo
Noter que cet algorithme n’est pas la traduction du diagramme de transitions de l’automate en une sorte d’ordinogramme.
L’état du système est mémorisé dans une variable qui doit conserver de façon permanente sa valeur.
A titre d’exemple donnons le squelette de ce qui pourrait être le point de départ de la réalisation d’une calculette.
On souhaite réaliser une calculatrice simple, disposant des quatre opérations de base agissant sur des nombres " à virgule ", c’est à dire sans les exposants. Un tel objet doit évidemment traiter correctement les priorités entre opérateurs :
2 + 3 * 4 => 14
2 * 3 + 4 => 10 etc.
Notre machine hypothétique dispose d’une entrée qui lit un caractère au clavier. Lecture " au vol ", c’est à dire que le caractère est envoyé sans attendre la frappe d’un caractère spécial du style retour chariot ou équivalent. Pour CVI, par exemple, cette fonction s’appelle getkey(), si vous préférez Borland vous utiliserez getch() (version sans écho, notre programme complet gère l’écho à l’écran).
Analyse de quelques problèmes à traiter :
Un petit problème se pose immédiatement : si je tape 3.1416+2 comment faire pour reconnaître que le chiffre ‘6’ appartient bien au nombre Pi, mais que le symbole ‘+’ qui le suit est un opérateur d’addition. Nous n’allons évidemment pas demander à l’utilisateur de taper un espace, ou n’importe quoi d’autre, il a le droit d’être bête. Nous nous chargerons de l’opération. Pour trouver la fin du nombre il a bien fallu lire le caractère ‘+’, mais pour traiter la suite il faut le redéposer sur le clavier ! Les librairies C sous Unix permettent de faire cette " délecture ", nous devrons ici nous en charger nous même (fonction clavier(action, valeur)).
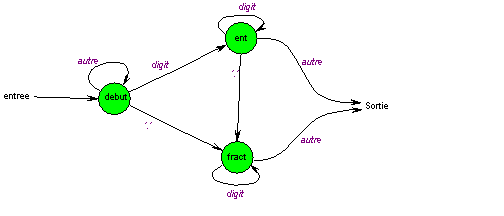
Autre point amusant : comment reconnaître qu’un nombre est bien construit ? En fait il suffit de le décrire : " un nombre commence par un chiffre ou un point (décimal). Suivent des chiffres ou, si le premier caractère était un chiffre, des chiffres suivis d’un point suivi de chiffres. Le premier caractère qui viole cette règle indique la fin du nombre. ". Cette phrase suffit pour écrire un automate qui décrit la grammaire d’un nombre (fonction lire_val(adresse_valeur)).
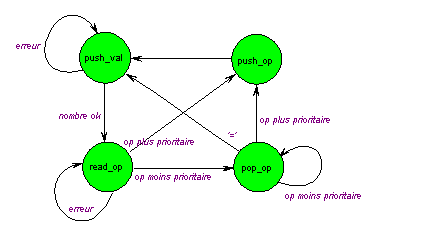
Pour traiter la grammaire d’une expression c’est un peu plus compliqué. La priorité des opérateurs impose de mettre des opérations en attente pour traiter d’abord des opérations plus prioritaires. Une façon (il y en a des dizaines, dont trois ou quatre propres) de traiter le problème est de créer une pile d’opérations en attente. C’est ce que font certains fabriquants de calculettes pédantes qui imposent à l’utilisateur de penser " postfixé ". Nous ne suivrons évidemment pas cet exemple, nous gérerons la pile d’opérations en attente nous même.

Le programme (non certifié) est fourni ci-dessous.
// calc_4op.c
// calculette quatre opérations, automate et pile
#include <ansi_c.h>
#define MAX_OPE 3
#define MAX_VAL 4
int lire_val(double *) ;
int lire_op(ope *) ;
void calcule(double *, char) ;
typedef enum {push_val,read_op,push_op,pop_op} cal_type ; // les états
cal_type calc = push_val ; // le registre d’état lui-même
// pile opérateur priorite min en fond de pile
typedef struct {char op; char pri;} ope ;
ope pile_ope[MAX_OPE] = {0} ;
ope *top_ope = pile_ope ;
double pile_val[MAX_VAL] ; // la pile opérandes
double *top_val = pile_val - 1 ; // fond de pile vide
void main(void)
{
ope code ; // l’opérateur courant lu au clavier
int bidon ; // nécessaire à la syntaxe de la fonction clavier
while(1)
{
switch(calc)
{
case push_val : if(lire_val(++top_val)) calc = read_op ;
// valeur correcte
else // erreur
{
top_val-- ; // erreur : on annule l'entree
clavier(prendre,&bidon) ;
}
break ;
case read_op : if(lire_op(&code) != -1) // operateur legal
if(code.pri > top_ope->pri) calc = push_op ;
else calc = pop_op ;
break ;
case push_op : *++top_ope = code ;
putchar('\n') ;
putchar(code.op) ;
calc = push_val ;
break ;
case pop_op : if(code.pri > top_ope->pri)
if(code.op == '=') // fond de pile , operateur '='
{
top_ope = pile_ope ;
top_val = pile_val ;
calc = push_val ;
}
else calc = push_op ; // on empile
else
{
calcule(top_val--,(top_ope--)->op) ;
printf("\n=%lf",*top_val) ;
}
break ;
}
}
}
// traitement des opérateurs :
int lire_op(ope *ad_code)
{
int code ;
clavier(prendre,&code) ;
ad_code->op = code ;
switch(code)
{
case '-' :
case '+' : ad_code->pri = 2 ;
return 1 ;
case '/' :
case '*' : ad_code->pri = 3 ;
return 1 ;
case '=' : ad_code->pri = 1 ;
return 1 ;
case 'q' : exit(0) ;
default : return -1 ; // caractère inattendu
}
}
// Opérations arithmétiques effectuées sur le sommet de la pile :
void calcule(double *pile, char op_code)
{
switch(op_code)
{
case '+' : *(pile - 1) = *pile + *(pile - 1) ;
break ;
case '-' : *(pile - 1) = *(pile - 1) - *pile ;
break ;
case '*' : *(pile - 1) = *pile * *(pile - 1) ;
break ;
case '/' : if(*pile) *(pile - 1) = *(pile -1) / *pile ;
else printf("\ndivision par zero\n") ;
break ;
}
}
Comme la calculette elle-même, les fonctions de gestion du tampon clavier et de reconnaissance d’un nombre font appel à des automates :
#include <utility.h>
#include <ansi_c.h>
int lire_val(double *) ;
typedef enum {poser,prendre} gestion_buf ;
typedef enum {plein,vide} etat ;
void clavier(gestion_buf, int *val) ;
// clavier.c
#include "clavier.h"
// Gestion de la lecture clavier avec un tampon d’un caractère
void clavier(gestion_buf action, int *val)
{
static etat etat_tampon = vide ;
static int tampon ;
switch(etat_tampon)
{
case vide : if(action == prendre)
{
*val = GetKey() ;
// putchar((char)*val) ; // pour avoir l'echo local
}
else
{
tampon = *val ;
etat_tampon = plein ;
}
break ;
case plein :if(action == prendre)
{
*val = tampon ;
etat_tampon = vide ;
}
break ;
}
}
// reconnaissance d’un nombre
int lire_val(double *ad)
{
double valeur ;
static char buf[128] ;
int caract,i ;
typedef enum {debut,fract,ent} gestion_nbre ;
gestion_nbre etat ;
etat = debut ;
i = 0 ;
while(i < 127)
{
clavier(prendre,&caract) ; // accepter un caractère
if(caract == 'q') exit(0) ; // on peut meme terminer le programme
switch(etat)
{
case debut :if(isdigit((char)caract ))
// un nombre peut débuter par un chiffre...
{
buf[i++] = caract ;
putchar(caract) ;
etat = ent ; // on continue sur une partie entière
}
else if(caract == '.') //...ou par un point décimal
{
buf[i++] = caract ;
putchar(caract) ;
etat = fract ;
// on continue sur une partie fractionnaire
}
break ; // on ignore les autres caractères
// partie fractionnaire : des chiffres
case fract :if(isdigit((char)caract ))
{
buf[i++] = caract ;
putchar(caract) ;
}
else // fin de la partie fractionnaire
{
buf[i] = 0 ; // on termine la chaine
i = 127 ; // on force une sortie de boucle
clavier(poser,&caract) ;
// on repose le caractère ignoré
}
break ;
// partie entière : des chiffres ...
case ent : if(isdigit((char)caract ))
{
buf[i++] = caract ;
putchar(caract) ;
}
else if(caract == '.') //...ou par un point décimal
{
buf[i++] = caract ;
putchar(caract) ;
etat = fract ;
// on continue sur une partie fractionnaire
}
else // fin d'un nombre entier
{
buf[i] = 0 ; // on termine la chaine
i = 127 ; // on force une sortie de boucle
clavier(poser,&caract) ;
// on repose le caractère ignoré
}
break ;
}
}
return sscanf(buf,"%lf",ad) ; // la paresse perdra l’auteur
}
La variable etat_tampon de la fonction clavier() doit conserver la mémoire de l’état du tampon (et de son contenu) entre deux appels successifs, elle doit donc être statique. Les appels à la fonction clavier() proviennent, en pratique, de fonctions différentes d’un programme. Par exemple : 3.14+… doit être interprété comme le nombre 3.14 suivi d’une addition. Le caractère ‘+’ indique à la fonction de lecture d’un nombre que ce nombre est terminé. Ce même caractère doit pouvoir être relu par une autre fonction qui interprète sa signification en terme d’opérateur.
Il est parfois intéressant de déplacer hors du code de l’automate le calcul de l’état futur en faisant appel à une fonction de transitions. Le programme prend alors une forme très régulière, dans chaque état contient quelque chose du genre :
etat = fonc_transit(etat) ;
Si la fonction de transitions utilise une table de transitions (voir automates matériels), elle peut servir à créer uune famille d’automates similaires qui ne diffèrent que par le contenu de la table.
Les automates finis ou machines à nombre fini d’états (Finite state machines), en abrégé machines d’états, ou, encore, séquenceurs câblés, sont largement utilisées dans les fonctions logiques de contrôle, qui forment le coeur de nombreux systèmes numériques : arbitres de bus, circuits d’interfaces des systèmes à base de microprocesseurs, circuits de gestion des protocoles de transmission, systèmes de cryptages etc. Plus prosaïquement, la quasi totalité des fonctions séquentielles standard, compteurs, par exemple, peuvent être analysées, ou synthétisées, en adoptant le point de vue " automates ".
Une machine d’états est un système dynamique (i.e. évolutif) qui peut se trouver, à chaque instant, dans une position parmi un nombre fini de positions possibles. Elle parcourt des cycles, en changeant éventuellement d’état lors des transitions actives de l’horloge, dans un ordre qui dépend des entrées externes, de façon à fixer sur ses sorties des séquences déterminées par l’application à contrôler.
Un programmateur de machine à laver en est l’illustration typique : suite à la mise en marche, le programmateur contrôle que la porte est fermée, si oui il commande l’ouverture de la vanne d’arrivée de l’eau, quand la machine est pleine etc.
L’architecture générale d’une machine d’états simple est celle de la figure 4-1 :
Figure -1
Ce synoptique général va nous servir, éventuellement légèrement modifié, de support dans les explications qui suivent.
Le registre d’état, piloté par son horloge, constitue le coeur d’une machine d’états, les autres blocs fonctionnels, bien que généralement nettement plus complexes, sont " à son service ".
Le registre d’état est constitué de n bascules synchrones, nous admettrons dans ce qui suit, sauf précision contraire, que ce sont des bascules D, ce qui n’impose aucune restriction de principe, puisque nous savons passer d’un type de bascule à un autre.
Le contenu du registre d’état représente l’état de la machine, il s’agit d’un nombre codé en binaire sur n bits, dans un code dont nous aurons à reparler.
L’entrée du registre d’état constitue l’état futur, celui qui sera chargé lors de la prochaine transition active de l’horloge. Le registre d’état constitue la mémoire de la machine, l’élément qui matérialise l’histoire de son évolution.
L’importance de ce registre est telle que beaucoup de circuits programmables offrent la possibilité de le charger, à des fins de tests, avec une valeur arbitraire, indépendante du fonctionnement normal de la machine. Toute procédure de test devra s’appuyer sur la connaissance du contenu de ce registre, par une mesure réelle, ou en simulation.
La taille du registre d’état fixe évidemment le nombre d’états accessibles à la machine. Si n est le nombre de bascules et N le nombre d’états accessibles, ces deux nombres sont reliés par la relation :
N = 2n
Cette relation, qui ne présente guère de difficulté, est pourtant trop souvent oubliée des concepteurs débutants :
Le rôle de l’horloge, dans une réalisation synchrone, est de supprimer toute possibilité d’aléas dans l’évolution de l’état. Idéalement, entre deux transitions actives de l’horloge le système est figé, en position mémoire, son état ne peut pas changer. Dans la réalité, le temps de latence qui sépare deux fronts consécutifs du signal de l’horloge est mis à profit pour permettre aux circuits combinatoires d’effectuer leurs calculs, sans que les temps de retards, toujours non nuls, ne risquent de provoquer d’ambiguïté dans le résultat.
Ce qui a été dit à propos des bascules élémentaires se généralise : chaque transition d’horloge est suivie d’une période de grand trouble dans la valeur de l’état futur, le concepteur doit s’assurer que cette valeur est stable quand survient la transition d’horloge suivante (figure 4-2) :
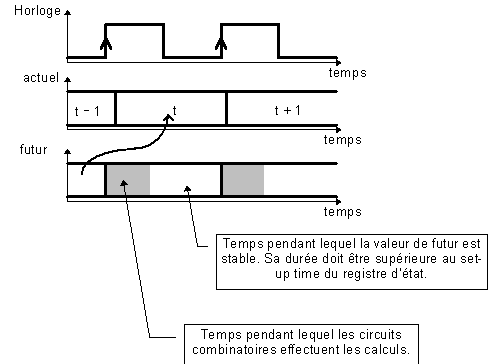
Figure -2
Sauf pour le calcul des limites de fonctionnement du système, le temps devient une variable discrète, un nombre entier qui indique simplement combien de périodes d’horloges se sont écoulées depuis l’instant pris comme origine.
Une machine d’états est complètement décrite par une équation de récurrence, qui permet de connaître le contenu du registre d’état à l’instant t, t entier, en fonction de ses valeurs précédentes et de celles des entrées.
Dans une architecture comme celle de la figure 4-1, l’équation de récurrence évoquée précédemment est du premier ordre (la portée temporelle de la mémoire est égale à une période d’horloge) :
Etat_actuel(t) = Etat_futur(t - 1)
Or la fonction logique combinatoire, f( ), qui calcule l’état futur, fournit une valeur qui dépend de l’état présent et des entrées, d’où la relation générale qui décrit l’évolution d’une machine d’états :
Etat_actuel(t) = f( Etat_actuel(t - 1) , Entrées(t - 1) )
Cette équation est la généralisation de celles qui ont été introduites à propos des bascules élémentaires.
Il est important de noter que, si l’équation qui régit l’évolution du registre d’état, pris dans son ensemble, est du premier ordre, ce n’est pas vrai pour l’équation d’évolution d’une bascule qui est, elle, plus complexe. Toutes les bascules du registre d’état sont, en général, couplées. L’ordre de l’équation d’évolution d’une bascule peut atteindre n, où n est la taille du registre d’état.
Pour illustrer ce qui précède, considérons le schéma de la figure 4-3 :

Figure -3
L’état du système est (Q1,Q0), ensemble constitué des états individuels des deux bascules. On admet que l’entrée extérieure div est synchrone de l’horloge. A chaque front montant du signal d’horloge hor, le système évolue suivant le système d’équations :
![]()
![]()
On peut remarquer, en passant, que l’équation de chaque bascule est effectivement du deuxième ordre, par exemple pour Q1 :
![]()
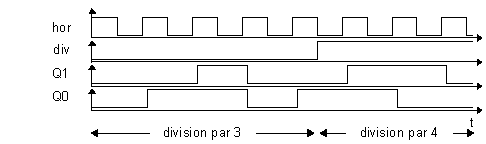
Figure -4
Sur le chronogramme de la figure 4-4, construit à partir des équations précédentes, on voit que :
Si les chronogrammes permettent d’illustrer un fonctionnement, ils ne constituent pas une méthode efficace d’analyse, et, encore moins, de synthèse. Dans l’étude de machines d’états simples, les diagrammes de transitions constituent une approche plus compacte, donc plus puissante, tout en fournissant exactement le même niveau de détails.
Dans un diagramme de transitions, on associe à chaque valeur possible du registre d’état, une case. Comme pour les bascules élémentaires, une transition est effectuée si trois conditions sont réunies :
Si aucune transition n’est active, le système reste dans son état initial. S’il n’y a pas d’ambiguïté le signal d’horloge est généralement omis (horloge unique), mais il conditionne toutes les transitions.
Reprenant l’exemple précédent, nous représentons, figure 4-5, le diagramme de transitions du diviseur par trois ou quatre. Le registre d’état contient deux bascules, soit quatre états accessibles. Pour chaque état initial, les équations du diviseur fournissent l’état d’arrivée.
Dans cet exemple, quel que soit l’état de départ, et quelle que soit la valeur de l’entrée div, il y a toujours une transition active ; le système change donc d’état à chaque front montant du signal d’horloge.
Quand le diviseur est dans l’état 3 le chemin parcouru dépend de la valeur de l’entrée div. Si div = '0' un cycle complet contient trois états, d’où la division de fréquence par trois, si div = '1', un cycle complet comporte quatre états, d’où la division de fréquence par quatre.
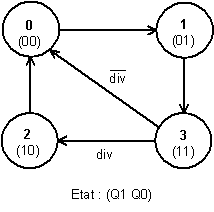
Figure -5
Dans l’exemple précédent, nous sommes partis des équations d’un système pour aboutir au diagramme de transitions qui en décrit le fonctionnement. Il s’agit là d’un travail d’analyse. Le concepteur se trouve généralement confronté au problème inverse : du cahier des charges il déduit un diagramme de transitions, et de ce diagramme il souhaite tirer les équations de commandes des bascules du registre d’état, ou une description en VHDL.
Rajoutons à l’exemple précédent une commande supplémentaire, en, telle que :
Le diagramme de transitions devient (figure 4-6) :
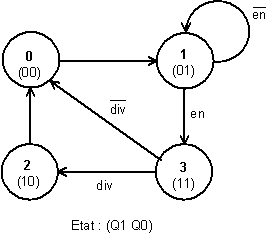
Figure -6
Quand le nombre de bascules du registre d’état et le codage des états sont connus, le passage du diagramme de transitions aux équations de commandes des bascules est immédiat. Les détails des calculs dépendent du type de bascules utilisées pour réaliser le registre d’état.
Avec des bascules D :
Il suffit de recenser, pour chaque bascule, toutes les transitions, et les maintiens, qui conduisent à la mise à '1' de la bascule. Dans notre exemple il y a deux bascules :
D’où, en notant les états de façon symbolique par leur numéro souligné, et en simplifiant, éventuellement les expressions obtenues :
![]()
![]()
Avec des bascules T :
Il suffit de recenser, pour chaque bascule, toutes les transitions qui conduisent à un changement d’état de la bascule. Dans notre exemple il y a deux bascules :
D’où, en notant les états de façon symbolique par leur numéro souligné et en simplifiant, éventuellement les expressions obtenues :
![]()
![]()
La comparaison entre les deux solutions, bascules D ou bascules T, montre que dans l’exemple considéré, la première solution conduit à des équations plus simples (ce n’est pas toujours le cas). Certains circuits programmables offrent à l’utilisateur la possibilité de choisir le type de bascules, ce qui permet d’adopter la solution la plus simple.
Pour passer d’un diagramme de transitions aux équations de commandes des bascules, le concepteur débutant peut toujours recourir à une table de vérité qui récapitule toutes les transitions possibles.
Si cette méthode est systématique, elle présente évidemment l’inconvénient d’être fort lourde. Le nombre de variables d’entrées de la table devient vite, même pour des problèmes simples, très élevé.
Le tableau qui suit correspond à la dernière version de notre diviseur par trois ou quatre. Quand, pour une transition, la valeur d’une commande est indifférente, elle apparaît par la valeur 'x'.
|
Etat initial |
Entrées |
Etat final |
|||
|
Q1 |
Q0 |
en |
div |
D1 |
D0 |
|
0 |
0 |
x |
x |
0 |
1 |
|
0 |
1 |
0 |
x |
0 |
1 |
|
0 |
1 |
1 |
x |
1 |
1 |
|
1 |
1 |
x |
0 |
0 |
0 |
|
1 |
1 |
x |
1 |
1 |
0 |
|
1 |
0 |
x |
x |
0 |
0 |
Table de transitions du diviseur par 3/4.
Cette table n’apporte rien de plus que le diagramme de transitions, son utilité est d’autant plus discutable que l’on effectue rarement les calculs à la main, et nous verrons qu’il est très simple de passer directement d’un diagramme de transitions au programme VHDL correspondant.
Nous avons vu que pour représenter, de façon non ambiguë le fonctionnement d’un système, un diagramme de transitions doit respecter certaines règles qui concernent les états, d’une part, et les transitions, d’autre part. Leur non respect constitue une erreur :
Ces deux derniers points méritent des éclaircissements ; leur non respect, qui ne saute pas toujours aux yeux, est l’une des principales sources d’erreur dans les diagrammes de transitions. Précisons cela en modifiant quelque peu le diviseur étudié précédemment.
On souhaite remplacer, dans le diviseur par 3/4, les commandes en et div par deux commandes, div3 et div4, actives à '1', qui fournissent globalement les mêmes fonctionnalités, mais avec une répartition des rôles un peu différente :
Deux versions du diagramme de transitions de la nouvelle variante du diviseur sont représentées figure 4-7.
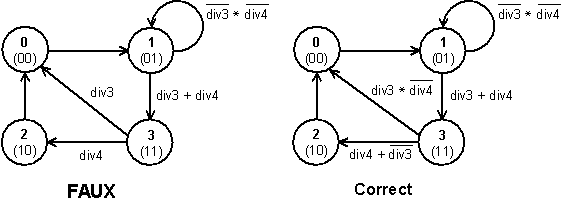
Figure -7
Sur les deux versions on a indiqué que le maintien dans l’état 1 est bien obtenu par complémentation de la condition de cet état, ce qui est correct.
La première version, marquée comme fausse sur la figure, contient deux erreurs qui concernent l’évolution à partir de l’état 3 :
La deuxième version présente une solution correcte au problème, l’erreur de syntaxe a disparu, et on a établi une priorité de la division par quatre. Si les deux commandes sont actives la machine prend le chemin de la division par quatre ; elle réagit de même si les deux commandes deviennent inactives alors que l’état 3 est actif, elle évolue vers l’état 1, pour s’y arrêter, en passant par les états 2 et 0.
Ce genre d’erreurs est vite arrivé. Lors de la traduction en VHDL d’un diagramme de transitions les erreurs de syntaxe disparaissent le plus souvent, grâce aux priorités qu’introduisent les algorithmes séquentiels :
Mais la disparition des erreurs de syntaxe peut, malheureusement, s’accompagner d’une modification du sens qu’avait prévu un concepteur insuffisamment rigoureux.
Un état piège est un état dans lequel la machine peut entrer, mais dont elle ne sort jamais, comme un piège à anguilles. Cela peut être volontaire, aboutissement d’une séquence d’initialisation qui suit la mise sous tension d’un système, par exemple ; mais c’est rare. De plus dans ce genre de situation, l’état piège est explicite, il est donc visible. Plus dangereux sont les pièges cachés, qui ne figurent pas sur le diagramme de transitions.
Prenons un exemple.
On souhaite réaliser, au moyen de deux bascules, deux signaux rigoureusement synchrones, issus de deux diviseurs de fréquence par deux couplés, tels que les sorties des bascules soient toujours complémentaires.
La première version du diagramme de transitions de la figure 4-8 semble convenir, a tort.
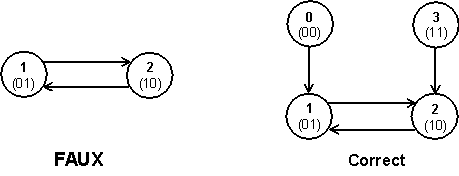
Placé dans un circuit programmable de type 16V8, l’automate ainsi créé ne fonctionne pas du tout :
La deuxième version fonctionne correctement, et a, de plus, la vertu d’être décrite par des équations plus simples, que l’on aurait d’ailleurs pu trouver directement par un simple raisonnement qualitatif.
Le problème des pièges cachés a conduit à l’introduction, dans les langages de description, de sortes de " méta états ", qui regroupent tous les non-dits, pour pouvoir préciser ce qui doit leur arriver (else d’un if, others d’un case, en VHDL). Mais, comme l’exemple précédent le montre, le raccordement de tous les états inutilisés dans un même état du diagramme, ne conduit pas toujours à la solution la plus simple.
VHDL offre de multiples possibilités pour traduire le fonctionnement d’un automate. Seules nous intéressent ici les descriptions comportementales, dans lesquelles le coeur d’un automate est associé à un processus.
Même avec cette restriction, qui exclut les représentations structurelles, toujours possibles, le langage offre des styles de programmation variés, qui permettent de traduire simplement les situations les plus diverses.
Nous tenterons, ci-dessous, de donner certaines indications générales, qui peuvent servir de guide pour les cas les plus courants. En conformité avec ce qui a été dit au début de ce chapitre, nous ne nous occuperons que de fonctions synchrones, dont le synoptique général correspond à celui de la figure 4-1.
A tout seigneur tout honneur, nous commencerons par le registre d’état.
Il est matérialisé, dans un programme source en VHDL, par deux éléments indissociables :
Le choix du type employé pour le signal d’état dépend de la nature des opérations les plus fréquemment rencontrées dans le diagramme de transitions, du lien entre le registre d’état et les sorties, nous reviendrons sur ce point important, et ... du goût du concepteur. Même s’il semble plus naturel d’adopter, par exemple, un type entier pour une machine dont le fonctionnement se modélise bien par des opérations arithmétiques, il est bon de se souvenir que les opérateurs peuvent être surchargés, pour agir sur des vecteurs de bits. Les paquetages fournis avec un compilateur contiennent déjà la plupart de ces surcharges utiles.
Faut il créer un processus à part pour la fonction combinatoire f( ), qui calcule, dans le synoptique de la figure 4-1, l’état futur ? Rien n’est moins sûr.
La séparation du registre d’état et de sa commande conduit à un premier processus, qui est trivial, pour le registre d’état, et à un second processus, qui l’est beaucoup moins, pour la commande. Notons, en particulier, que des combinaisons des entrées dont on ne précise pas l’effet sur la machine génèrent, par défaut, des maintiens dans la version mono processus, et des mémorisations asynchrones des commandes dans la version à deux processus séparés !
Un exemple de prototype de machine d’états qui corresponde au synoptique de la figure 4-1 peut être :
entity proto_machine is
generic (n , p , q : integer := 2 ) ;
port(hor : in bit ;
entrees : in bit_vector(0 to p - 1);
sorties : out bit_vector(0 to q - 1) ) ;
end proto_machine ;
-- suivant le compilateur utilise :
use work.paquetage_arithmetique.all ;
architecture comporte of proto_machine is
signal etat : bit_vector(n - 1 downto 0) ;
begin
machine : process
begin
wait until hor = '1' ;
-- ci-dessous code du diagramme de transitions.
end process machine ;
actions : process
begin
-- ci-dessous code du calcul des sorties.
end process actions ;
end comporte ;
L’activation d’une transition, dans un diagramme d’états, dépend de l’état initial et des entrées extérieures. On peut, quitte à caricaturer un peu une réalité toujours plus nuancée, situer une machine d’états quelque part entre deux extrêmes :
Les deux discussions qui suivent correspondent à ces deux situations.
Pour décrire un diagramme de transitions en VHDL, une méthode simple consiste à traiter toutes les valeurs possibles de l’état de la machine, et pour chaque cas, analyser les entrées pour en déduire l’état suivant. L’exemple ci-dessous est la transcription, avec cette démarche, du diviseur par trois ou quatre étudié précédemment (diagramme de la figure 4-6).
entity div3_4 is
port ( hor , div , en : in bit ;
Q1 , Q0 : out bit ) ;
end div3_4 ;
architecture comporte of div3_4 is
signal etat : bit_vector(1 downto 0) ;
begin
Q1 <= etat(1) ;
Q0 <= etat(0) ;
process
begin
wait until hor = '1' ;
case etat is -- primauté a l’etat.
when "00" => etat <= "01" ;
when "01" => if en = '1' then
etat <= "11" ;
end if ;
when "10" => etat <= "00" ;
when "11" => if div = '1' then
etat <= "10" ;
else
etat <= "00" ;
end if ;
end case ;
end process ;
end comporte ;
La même fonction de principe, mais avec un nombre plus important d’états possibles, conduirait vite à une énumération d’une lourdeur prohibitive. La sélection others de l’instruction when permet, quand un traitement collectif de certains états est possible, de résoudre le problème.
Le programme qui suit correspond à un diviseur par 255/256, pour lequel on a abandonné la contrainte d’obtenir la même fréquence pour toutes les sorties, contrainte irréalisable avec un registre d’état de largeur 8 bits :
entity dual_modulus is
generic (n : integer := 8 ) ;
-- n est la taille du registre d’etat.
port(hor : in bit ;
en, div : in bit ;
sortie : out integer range 0 to 1 ) ;
end dual_modulus ;
architecture comporte of dual_modulus is
signal etat : integer range 0 to 2**n - 1 ;
begin
machine : process
begin
wait until hor = '1' ;
case etat is
when 1 => -- cas particulier.
if en = '1' then
etat <= etat + 1;
end if ;
when 2**n - 2 =>
if div = '0' then
etat <= 0 ;
else
etat <= etat + 1 ;
end if ;
when others => -- cas general.
etat <= etat + 1 ;
end case ;
end process machine ;
actions : process
begin
sortie <= etat / 2**(n-1);-- bit de poids fort.
end process actions ;
end comporte ;
L’exemple précédent illustre la limitation du dessin explicite d’un diagramme de transitions, dans des cas un peu complexes. Certains outils de CAO fournissent à l’utilisateur la possibilité de créer des " macro états ", utiles quand une partie du diagramme peut être décrite par une formule. Donnons un exemple (figure 4-9) qui correspond au diviseur par 255/256 précédent :
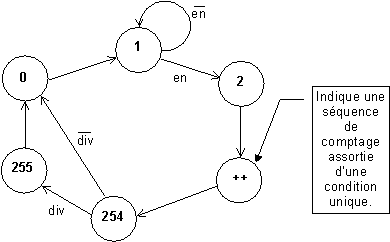
Figure -9
Ces extensions, qui ne sont absolument pas standardisées, à la représentation traditionnelle des diagrammes de transitions permettent de représenter de façon visuelle des fonctionnement complexes, ce n’est pas à négliger.
Les automates qui disposent de commandes globales, dont les actions peuvent être décrites indépendamment de la valeur explicite de l’état, se prêtent fort mal à une description aussi détaillée que celle fournie par un diagramme de transitions. Leur description purement algorithmique peut, pourtant, être fort simple.
L’exemple ci-dessous illustre ce fait au moyen d’un compteur modulo dix, inspiré du circuit 74162, pourvu de trois commandes clear, load et en, dans l’ordre de priorités décroissantes :
entity decade is
port ( hor , clear, load, en : in bit ;
donnee : in integer range 0 to 9 ;
sortie : out integer range 0 to 9 ) ;
end decade ;
architecture comporte of decade is
signal etat : integer range 0 to 9 ;
begin
machine : process
begin
wait until hor = '1' ;
if clear = '0' then -- primauté aux commandes.
etat <= 0 ;
elsif load = '0' then
etat <= donnee ;
elsif en = '1' then
case etat is -- un cas particulier.
when 9 => etat <= 0 ;
when others => etat <= etat + 1 ;
end case ;
end if ;
end process machine ;
sortie <= etat ;
end comporte ;
Il est clair qu’un diagramme de transitions complet d’un tel objet est pratiquement impossible à écrire : le chargement parallèle autorise des transitions entre toutes les paires d’états. L’approche algorithmique, par contre, ne pose aucune difficulté.
On notera également que la structure if...elsif...else...end if permet de traduire, de façon très lisible, la priorité qui existe entre les différentes commandes.
Résumons nous :
Les logiciels de synthèse libèrent le concepteur d’avoir à se préoccuper des détails des calculs qui conduisent, face à un problème posé, d’une idée de solution aux équations de commandes des circuits, déduites d’un diagramme de transitions ou d’un algorithme. Le travail de conception qui reste à sa charge réside principalement dans les choix généraux d’architectures : découpage du système en sous ensembles de taille humaine, choix de structures et de codages pour chaque sous ensemble. Ces derniers comprennent principalement le traitement des entrées - sorties et, en liaison avec les sorties, le type de codage des états.
Suivant la façon dont les sorties dépendent des états et des commandes, on distingue deux types d’automates : les machines de Moore et les machines de Mealy. Dans les premières les sorties ne dépendent que de l’état actuel de la machine, dans les secondes les sorties dépendent de l’état de la machine et des entrées.
Dans beaucoup de cas réels la séparation n’est pas aussi tranchée : certaines sorties sont traitées comme des sorties d’une machine de Moore, d’autres comme des sorties d’une machine de Mealy.
A l’image de M. Jourdain, nous avons, en réalité, fait des machines de Moore sans le savoir. Le synoptique général de la figure 4-1, dans lequel les sorties sont fonctions uniquement de la valeur du registre d’état, est la définition même d’une telle machine.
Dans ce type d’architecture, le calcul des sorties et le codage des états sont évidemment intimement liés. Nous aurons l’occasion de revenir sur ce point ultérieurement.
Dans une machine de Mealy les entrées du système ont une action directe sur les sorties, nous admettrons, dans un premier temps, que les sorties sont des fonctions purement combinatoires, symbolisées par une fonction g( ), des entrées et de l’état de la machine.
La structure générale d’une machine de Mealy est la suivante (figure 4-10) :
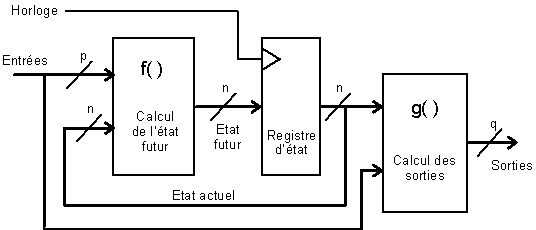
Figure -10
Une première différence apparaît alors immédiatement entre les comportements de sorties de Moore et de Mealy : les premières évoluent suite à un changement d’état, donc à la période d’horloge qui suit celle où a varié l’entrée responsable de l’évolution, les secondes réagissent immédiatement à une variation d’une entrée, précédant en cela l’évolution du registre d’état.
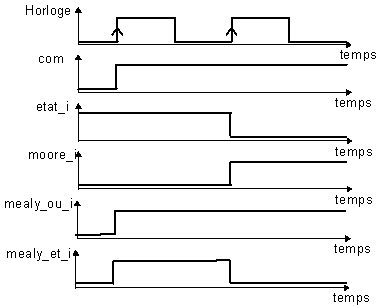
Figure -11
Le chronogramme de la figure 4-11 illustre ce point ; on y représente, en supposant le fonctionnement idéal, c’est à dire sans faire apparaître les temps de propagations :
mealy_ou_i = com + etat_arrivée,
où etat_arrivée est l’état qui suit etat_i,
mealy_et_i = com * etat_i.
Un point intéressant, que souligne ce chronogramme, est la possibilité de générer, par une sortie de Mealy, une impulsion qui dure une période d’horloge, indiquant qu’un changement d’état va se produire au front d’horloge suivant (sortie mealy_et_i).
Une application classique des machines de Mealy est la création d’opérateurs pourvus de sorties d’extension. Reprenons, à titre d’exemple, le compteur modulo 10 de l’exemple VHDL précédent. Il serait souhaitable de pouvoir associer simplement plusieurs de ces compteurs en cascade, de façon à réaliser un compteur sur plusieurs chiffres décimaux, un compteur kilométrique de voiture, par exemple, sans avoir à rajouter de circuiterie supplémentaire.
Pour cela il faut disposer d’une sortie, rco (pour ripple carry out), qui nous indique que la décade va passer à zéro, c’est à dire qu’elle est dans l’état 9 et qu’elle est autorisée à compter, car son entrée d’autorisation, en, est à un.
Mécanisme d’anticipation et influence directe d’une entrée, la sortie rco d’un compteur est bien une sortie de Mealy. Le programme ci-dessous contient la modification souhaitée :
entity decade_rco is
port ( hor , clear, load, en : in bit ;
donnee : in integer range 0 to 9 ;
sortie : out integer range 0 to 9 ;
rco : out bit ) ;
end decade_rco ;
architecture comporte of decade_rco is
signal etat : integer range 0 to 9 ;
begin
machine : process
begin
wait until hor = '1' ;
-- même code que précédemment.
end process machine ;
sortie <= etat ;
rco <= '1' when etat = 9 and en = '1' else '0';
end comporte ;
Pour créer un compteur à plusieurs chiffres décimaux, il suffit alors de connecter la sortie rco de chaque décade sur l’entrée en de la décade de poids supérieur ; il va sans dire que toutes les décades doivent être pilotées par la même horloge !
Pour tenir compte de l’action immédiate des entrées sur les sorties, dans une machine de Mealy, on complète parfois le diagramme de transitions de la machine en faisant figurer, en plus de la condition de transition, la valeur associée des sorties du type Mealy.
Par exemple, pour une simple bascule R-S synchrone, mais qui " réagit " instantanément, nous obtenons (figure 4-12) :
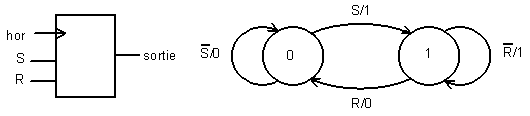
Figure -12
Un tel diagramme se lit de la façon suivante :
Quand la bascule est à 0, la sortie est à 0 tant que l’entrée S est à 0,
quand S passe à 1 la sortie passe à 1 et la bascule effectue la transition 0® 1 au front d’horloge suivant ;
quand la bascule est à 1, la sortie est à 1 tant que l’entrée R est à 0,
quand R passe à 1, la sortie passe à 0 et la bascule effectue la transition 1® 0 au front d’horloge suivant.
De ce diagramme nous pouvons déduire l’équation de la commande, D, de la bascule, et l’équation de la sortie :
![]()
![]()
Il se trouve que, dans cet exemple, l’équation de la sortie est identique, dans la forme mais pas dans le résultat), à celle de la commande de la bascule ; ce n’est évidemment pas toujours le cas.
Afin d’illustrer les différences entre les deux types de machines d’états, nous allons donner un exemple d’application, traité par les deux méthodes.
Un décodeur Manchester différentiel.
Dans les communications séries entre ordinateurs on utilise généralement des techniques particulières de codage pour les signaux qui circulent sur le câble, par exemple, le codage Manchester différentiel. En codage Manchester différentiel, chaque intervalle de temps élémentaire, pendant lequel un signal binaire est placé sur le câble, nommé le plus souvent " temps bit ", est divisé en deux parties de durées égales avec les conventions suivantes :
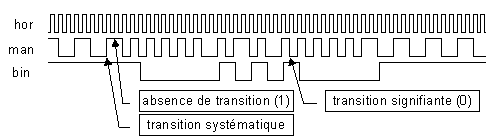
Figure -13
Le chronogramme de la figure 4-13 représente un exemple d’allure des signaux. Les données à décoder, le signal man, sont synchrones d’une horloge hor ; on souhaite réaliser un décodeur qui fournit en sortie le code binaire correspondant, bin. La sortie du décodeur est retardée d’une période d’horloge par rapport à l’information d’entrée, pour une raison qui s’expliquera par la suite.
Analyse du problème :
L’idée est assez simple, nous allons construire une machine d’états qui, parcourt un premier cycle quand le signal d’entrée change à chaque période d’horloge, ce qui correspond à un '0' transmis, et change de cycle quand elle détecte une absence de changement du signal d’entrée, qui correspond à un '1' transmis.
Machine de Mealy :
L’absence de changement peut se produire tant pour un niveau haut que pour un niveau bas du signal d’entrée, d’où l’ébauche de diagramme de transitions de la figure 4-14 (page suivante).
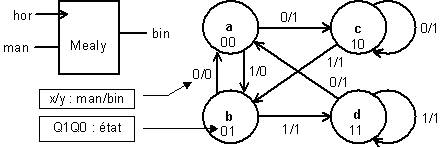
Figure -14
On se convaincra facilement que les cycles parcourus sont :
En fonctionnement permanent, une fois le système synchronisé et sauf erreur dans le code d’entrée, les conditions de maintien dans les états c et d sont toujours fausses, elles servent à la synchronisation en début de réception.
Du diagramme précédent on déduit les équations de commandes des bascules, D1 et D0, et celle de la sortie ; après quelques simplifications on obtient :
![]()
![]()
![]()
Machine de Moore (figure 4-15) :
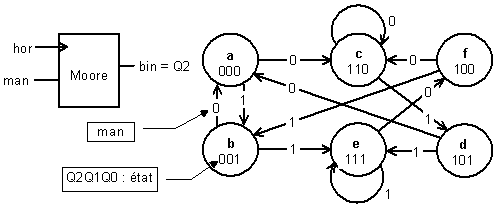
Figure -15
Dans une machine de Moore, différentes valeurs des sorties correspondent à des états différents, le diagramme de transitions doit donc contenir plus d’états.
Le diagramme ne représente pas deux états inutilisés, 2 et 3, en décimal. Leur affectation se fait lors du calcul des équations de commandes, de façon à les simplifier au maximum (si man = '1', 3® 7 et 2® 5 ; si man = '0', 3® 4 et 2® 6). On obtient, après quelques manipulations :
![]()
![]()
![]()
qui sont exactement les mêmes équations que celles obtenues dans le cas de la machine de Mealy, malgré l’apparente complexité du diagramme de transitions.
Comparaison :
Sur l’exemple que nous venons de traiter, il apparaît comme seule différence une bascule supplémentaire en sortie, pour générer le signal bin, dans le cas de la machine de Moore.
En regardant plus attentivement l’architecture des deux systèmes, on constate que la sortie combinatoire de la machine de Mealy risque de nous réserver quelques surprises : son équation fait intervenir des signaux logiques qui changent d’état simultanément, d’où des risques de création d’impulsions parasites étroites au moment des commutations. Une simulation confirme ce risque(figure 4-16) :
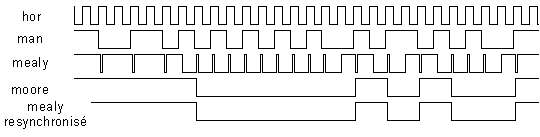
Quand on compare les sorties des deux machines, elles diffèrent d’une période d’horloge, ce qui est normal, mais la sortie de la machine de Moore est exempte de tout parasite, contrairement à celle de la machine de Mealy, ce qui est un avantage non négligeable.
L’élimination des parasites en sortie a une solution simple : il suffit de resyn-chroniser la sortie incriminée, c’est ce que nous avons fait pour obtenir la dernière trace du chronogramme précédent, dans ce cas, les deux approches conduisent à des résultats strictement identiques !
Autocritique.
Pour familiariser le lecteur aux raisonnements sur les diagrammes de transitions, avec un exemple pas tout à fait trivial, nous n’avons pas respecté la règle d’or du concepteur : diviser pour régner.
En séparant le problème en deux :
l’élaboration des diagrammes de transitions des deux machines d’état devient un exercice extrêmement simple.
Le programme VHDL de l’étude précédente :
On trouvera ci-dessous le programme VHDL qui contient, sous forme de deux processus, les deux solutions présentées pour le décodeur Manchester différentiel.
La lecture de ce programme doit se faire en observant parallèlement les deux diagrammes d’états.
entity mandec is
port ( hor, man : in bit ;
mealy , mealysync : out bit ;
moore : out bit );
end mandec ;
architecture comporte of mandec is
signal moore_state : bit_vector(2 downto 0);
signal mealy_state : bit_vector(1 downto 0);
begin
mealy <= mealy_state(1) or
not(mealy_state(0) xor man) ;
moore <= moore_state(2) ;
mealy_mach : process
begin
wait until hor = '1' ;
mealysync <= mealy_state(1) or
not(mealy_state(0) xor man) ;
case mealy_state is
when "00" => if man = '0' then
mealy_state <= "10" ;
else
mealy_state <= "01" ;
end if ;
when "01" => if man = '0' then
mealy_state <= "00" ;
else
mealy_state <= "11" ;
end if ;
when "10" => if man = '1' then
mealy_state <= "01" ;
end if ;
when "11" => if man = '0' then
mealy_state <= "00" ;
end if ;
end case ;
end process mealy_mach ;
moore_mach : process
begin
wait until hor = '1' ;
case moore_state is
when O"0" => if man = '0' -- etats en octal
then
moore_state <= O"6" ;
else
moore_state <= O"1" ;
end if ;
when O"1" => if man = '0' then
moore_state <= O"0" ;
else
moore_state <= O"7" ;
end if ;
when O"6" => if man = '1' then
moore_state <= O"5" ;
end if ;
when O"7" => if man = '0' then
moore_state <= O"4" ;
end if ;
when O"4" => if man = '0' then
moore_state <= O"6" ;
else
moore_state <= O"1" ;
end if ;
when O"5" => if man = '0' then
moore_state <= O"0" ;
else
moore_state <= O"7" ;
end if ;
when O"2" => if man = '0' -- etat inutiles
then
moore_state <= O"6" ;
else
moore_state <= O"5" ;
end if ;
when O"3" => if man = '0' then -- bis
moore_state <= O"4" ;
else
moore_state <= O"7" ;
end if ;
end case ;
end process moore_mach ;
end comporte ;
Quand on utilise des circuits standard, des compteurs programmables, par exemple, pour réaliser une machine séquentielle, le codage des états du diagramme de transitions est, de fait, imposé par le circuit cible. Il en va tout autrement quand la dite machine doit être implantée dans un circuit programmable ou un ASIC. Libéré des contraintes liées à une quelconque fonction prédéfinie, le concepteur peut, à loisir, adapter le codage des états à l’application qu’il est en train de réaliser.
Le choix d’un code est particulièrement important quand on s’oriente vers la réalisation d’une machine de Moore. L’exemple du décodeur Manchester nous a appris que l’un des avantages de cette architecture réside dans la possibilité de générer les sorties directement à partir du registre d’état, donc dénuées de tout parasite lié à leur calcul. Mais, comme nous le verrons dans deux exemples, l’identification des sorties du système à celles des bascules du registre d’état ne suffit généralement pas pour définir le codage des états.
Ce choix du codage mérite une grande attention, il conditionne grandement la complexité de la réalisation, sa bonne adaptation au problème posé ; un choix judicieux conduira à un résultat simple et facilement testable, alors qu’aucun logiciel d’optimisation ne compensera des erreurs de décision à ce niveau.
Le nombre d’états nécessaires et le type de code adopté fixent, en premier lieu, la taille du registre d’état. Schématiquement, si n est la taille, en nombre de bits, du registre d’état, et Ne le nombre d’états nécessaires, ces deux nombres (entiers !) doivent vérifier la double inégalité :
n £ Ne £ 2n
Si l’inégalité de gauche n’est pas vérifiée, certaines bascules sont probablement inutiles ; quand cette inégalité se transforme en égalité, on utilise un code très " dilué ", une bascule par état, qui présente l’avantage de la lisibilité, mais le danger de générer en grand nombre des états accessibles inutilisés (rappelons ici qu’il y a toujours 2n états accessibles).
Si l’inégalité de droite n’est pas vérifiée, la tentative est sans espoir ; si elle se transforme en égalité, on utilise un encodage " fort ", auquel il faudra très probablement adjoindre des fonctions combinatoires de calcul des sorties ; on ne réalise pas que des compteurs binaires ou des codeurs de position absolue (code de Gray).
Les situations intermédiaires correspondent en général à des codes adaptés aux sorties.
Encodage " fort " ou code " dilué " ? En caricaturant un peu, on peut dire que les tenants de la première solution préfèrent les fonctions combinatoires, et que les seconds sont des adeptes des bascules. Il n’est pas évident, à priori, de prévoir la complexité des équations engendrées par tel ou tel code. On gagne souvent à suivre le fonctionnement " naturel " de la machine, et, surtout, on gagne à se souvenir que les ordinateurs, et leurs compilateurs, ne sont pas posés sur un bureau à titre de décoration ; ils permettent de voir très vite quelle est la complexité sous jacente d’un choix, sans pour celà tomber dans le BAO.
L’idée qui vient naturellement à l’esprit est de choisir le codage en fonction des sorties à générer. C’est souvent la méthode la plus souple, celle qui conduit aux équations les plus faciles à interpréter, et pas forcément plus compliquées que celles que l’on obtiendrait avec d’autres codes.
Une commande de feux tricolores.
Pour satisfaire à une tradition bien établie, nous prendrons comme premier exemple une commande de feux de circulation routière.
Un passage pour piétons traverse une avenue ; il est protégé par un feu tricolore qui fonctionne à la demande des piétons : En l’absence de toute demande, les feux sont à l’orange clignotant (un nombre Tor de secondes allumés, Tor secondes éteints). Quand un piéton souhaite traverser l’avenue, il est invité à appuyer sur un bouton, ce qui provoque le déclenchement d’une séquence (vue des voitures) :
Profitons de cet exemple pour subdiviser la solution du problème en sous ensembles. Trois blocs fonctionnels peuvent être identifiés :
Outre les commandes des feux proprement dites, le bloc principal fournit un signal d’initialisation (cpt) à la temporisation, qui doit durer une période d’horloge, et un signal d’annulation (raz) de la requête, mémorisée, d’un piéton.
Les signaux d’entrée de ce bloc sont la requête (piet) et les trois indications de durée Tor Tr et Tv ; nous supposerons que ces dernières passent à '1', pendant une période d’horloge, quand les durées correspondantes se sont écoulées.
D’où le synoptique de la figure 4-17 :
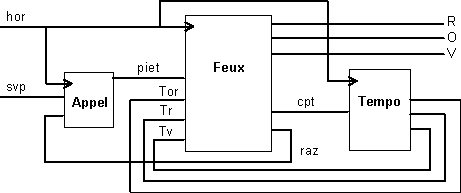
Figure -17
Nous nous contenterons d’étudier, ici, le bloc principal, feux, laissant la synthèse des deux autres blocs à titre d’exercice.
Première ébauche :
Le fonctionnement général peut être celui illustré par la figure 4-18 :
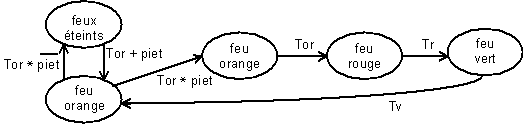
Figure -18
Précisions :
A partir de l’ébauche précédente, il nous reste à préciser le mode de calcul des signaux gérés par le processus feux, et à en déduire le codage des états. Le signal cpt se prête bien à une réalisation sous forme de sortie de Mealy, les signaux de commande des feux à une réalisation sous forme de sorties de Moore. Les deux états où le feu orange est allumé doivent être distingués, une bascule supplémentaire, qui n’est attachée à aucune sortie, doit être rajoutée à cette fin. La sortie raz peut être identique à la sortie qui correspond au feu rouge ; il n’est pas utile de mémoriser une demande de piéton quand les voitures sont arrêtées au feu rouge. D’où une version plus élaborée du diagramme de transitions (figure 4-19) :
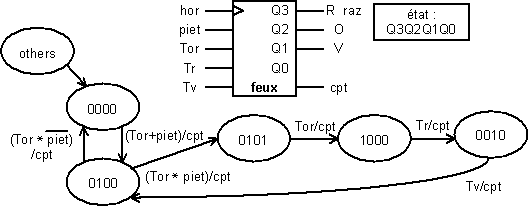
Figure -19
Programme VHDL :
Un exemple de programme VHDL, qui correspond au module feux uniquement, est fourni ci-dessous ; il se déduit directement du diagramme de transitions précédent.
entity feux is
port ( hor, piet, Tor, Tr, Tv : in bit ;
R, O, V, cpt : out bit );
end feux ;
architecture comporte of feux is
signal etat : bit_vector(3 downto 0) ;
begin
R <= etat(3) ;
O <= etat(2) ;
V <= etat(1) ;
machine : process -- diagramme de transitions.
begin
wait until hor = '1' ;
case etat is
when X"0" -- états en hexadécimal.
=> if (Tor or piet) = '1' then
etat <= X"4" ;
end if ;
when X"4" => if (Tor and piet) = '1' then
etat <= X"5" ;
elsif (Tor and not piet) = '1' then
etat <= X"0" ;
end if ;
when X"5" => if Tor = '1' then
etat <= X"8" ;
end if ;
when X"8" => if Tr = '1' then
etat <= X"2" ;
end if ;
when X"2" => if Tv = '1' then
etat <= X"4" ;
end if ;
when others => etat <= X"0" ;
-- pour les états inutilisés.
end case ;
end process machine ;
mealy : process -- calcul de la sortie cpt.
begin
wait on etat, piet, Tor, Tr, Tv ; -- liste de sensibilité
cpt <= '0' ; -- assure un bloc combinatoire.
case etat is
when X"0" => if Tor = '1' or piet = '1' then
cpt <= '1' ;
end if ;
when X"4" => if Tor = '1' then
cpt <= '1' ;
end if ;
when X"5" => if Tor = '1' then
cpt <= '1' ;
end if ;
when X"8" => if Tr = '1' then
cpt <= '1' ;
end if ;
when X"2" => if Tv = '1' then
cpt <= '1' ;
end if ;
when others => null ; -- case complet.
end case ;
end process mealy ;
end comporte ;
Le décodeur Manchester réexaminé.
Comme deuxième exemple, reprenons, en la complétant un peu, l’étude du décodeur Manchester différentiel. Nous avions omis, dans la version précédente, un deuxième signal de sortie, rx, qui indique aux utilisateurs la cadence de transmission. Comme on peut le voir sur la figure 4-20 , ce signal a une fréquence moitié de celle de l’horloge, mais il ne peut pas s’agir d’un simple diviseur par deux : un diviseur par deux est incapable de distinguer les transitions systématiques des transitions signifiantes du signal d’entrée man, il est incapable de se synchroniser.
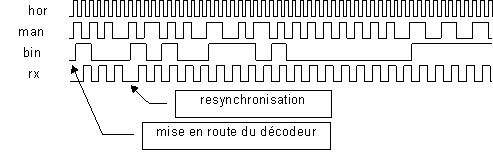
Figure -20
Choisissons, comme précédemment, la sortie Q2 (poids fort) du registre d’état pour générer le signal bin. Pour le signal rx, il est pratique de prendre la sortie Q0 de ce registre ; une fois le décodeur synchronisé, les trajets parcourus dans le diagramme de transitions doivent être tels que la parité du code de l’état change à chaque transition : le successeur d’un nombre impair doit être pair, et réciproquement. Le diagramme de la figure 4-7, étudié précédemment, ne respecte pas cette clause (transition a® c , par exemple), et ne peut pas la respecter, le nombre d’états n’étant pas suffisant (si on échangeait les codes des états a et b, par exemple, la transition e® a ne respecterait plus l’alternance de parité).
Partant du cycle c® d® e® f..., qui correspond aux transmissions de signaux binaires égaux à '1', on adjoint à ce cycle deux cycles équivalents, a® b® a...et g® h® g..., qui codent les '0' transmis, mais avec une parité inversée.
On obtient un diagramme à 8 états, qui peut, par exemple, être celui de la figure 4-21.
Comme précédemment, les conditions de maintien sont, en régime établi, toujours fausses. Leur détection pourrait servir à indiquer une faute de synchronisation.
Nous laisserons au lecteur le soin de traduire ce diagramme de transitions en équations de commandes des bascules, et en programme VHDL, ce qui ne pose guère de difficulté.
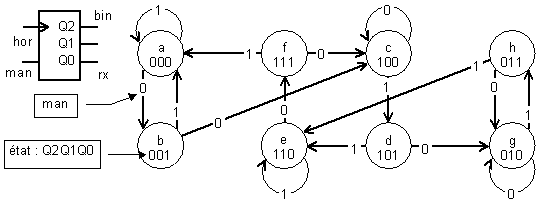
Figure -21
Bascules enterrées.
Dans les deux exemples précédents, certaines bascules servent de sorties, d’autres ne servent qu’aux états internes. De telles bascules sont dites bascules enterrées (burried flip flop). De nombreux circuits programmables offrent la possibilité d’utiliser des bascules enterrées ; cela a l’avantage de diminuer, pour une complexité de circuit donnée, le nombre de broches d’accès nécessaires. Il est clair, cependant, que ces circuits sont plus délicats à tester : les états ne sont pas tous visibles en sortie.
Les codes dits un seul actif (one hot), sont les plus dilués : à chaque état on attribue une bascule ; la machine étant, par définition, dans un seul état à la fois, si l’une des bascules est active, toutes les autres sont inactives. La commande de feux, étudiée au paragraphe précédent, serait une commande de ce type si on n’avait pas eu la fantaisie d’y rajouter une bascule enterrée.
C’est le code classique des compteurs, nous l’avons rencontré, par exemple, à l’occasion du diviseur à double rapport de division 255/256.
C’est typiquement le code que l’on obtient quand on réalise des machines d’états avec des fonctions standard.
On dit qu’un code est adjacent, dans le cas d’une machine d’état, si pour toutes les transitions du diagramme d’états, le changement de valeur du registre d’état ne porte que sur un chiffre binaire.
Très en vogue quand on synthétisait des automates asynchrones, ces codes ont perdu de l’importance avec la généralisation des techniques synchrones. La contrainte que représente le respect de l’adjacence, pour tous les états successifs, devient rapidement très difficile à observer.
On peut, malgré tout noter que, si cela ne complique pas, par ailleurs, le problème, c’est souvent une bonne idée de respecter l’adjacence dans les transitions, au moins partiellement.
Tous les codes qui n’occupent pas la totalité des états accessibles génèrent des états inutilisés. Notre feu rouge de tout à l’heure, par exemple, utilisait cinq des seize états disponibles. Le non raccordement des états inutilisés dans l’un des états du cycle relèverait, dans ce cas de la roulette russe, mais avec les deux tiers des logements du barillet du révolver chargés.
Si on n’est pas certain que les états inutilisés rejoignent naturellement l’un des états utiles du diagramme de transitions, il faut obligatoirement leur adjoindre une transition qui les ramène dans un territoire connu, faute de quoi on risque de créer une machine qui se " plante " à la première occasion.
Lors de la première ébauche d’un diagramme de transitions, il peut arriver que l’on crée des états inutiles. Cela n’est pas, en soi, dramatique, mais il peut être intéressant de les rechercher quand, notamment, l’économie d’un ou deux états permet de réduire la taille du registre d’état.
Quand deux états sont ils équivalents ?
Quand ils génèrent les mêmes sorties et les mêmes valeurs futures des sorties, quelles que soient les séquences d’entrée.
Derrière cette définition, fort simple en apparence, se cache parfois une grande difficulté de mise en pratique de cette recherche.
Un cas particulier simple à identifier se rencontre assez souvent sur des diagrammes de transitions de dimension raisonnable : deux états fournissent les mêmes sorties et ont les mêmes états futurs, ils sont alors équivalents, on peut supprimer l’un d’entre eux.
Nous n’envisageons que la réalisation des machines d’états synchrones. Cela veut dire qu’au niveau local toutes les bascules qui interviennent sont pilotées par une horloge unique. Il est clair qu’au niveau d’un système cette règle du synchronisme absolu est rarement observée, elle nuirait à la modularité des sous ensembles.
Lors des échanges entre sous ensembles pilotés par des horloges différentes, ou pour des interfaces avec un monde extérieur qui ne possède pas d’horloge du tout, un piéton, par exemple, la question de la synchronisation des signaux d’entrée et de sortie se pose.
Les sorties calculées par des fonctions logiques combinatoires génèrent des impulsions parasites, nous en avons vu un exemple avec le décodeur Manchester. Totalement inoffensives si elles sont exploitées par un système piloté par la même horloge, ces impulsions peuvent être fort mal acceptées par un récepteur asynchrone de l’horloge locale.
Des bascules de synchronisation des sorties suppriment ce défaut, elles assurent des signaux stables entre deux fronts d’horloge.
L’adjonction pure et simple de bascules en sortie, à la place du bloc de calcul des sorties du synoptique de la figure 4-1, retarde d’une période d’horloge les valeurs des sorties par rapport à celles du registre d’état. Si ce retard présente un inconvénient, il est toujours possible, quitte à alourdir la partie combinatoire de la réalisation, d’anticiper le calcul des sorties en utilisant pour leur calcul l’état futur au lieu de l’état actuel.
Le synoptique de la figure 4-1 devient alors (figure 4-22) :
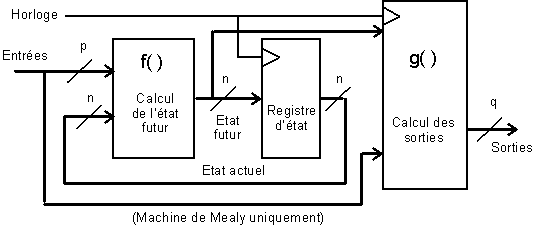
Figure -22